| Главная » Статьи » На пальцах |
Понятие о формуле дифференцирования назад (BDF)При анализе динамических режимов электрических цепей необходимо получить решение дифференциально–алгебраической системы уравнений: Число производных в системе (1) может быть меньше числа неизвестных токов и напряжений, то есть m≤n, число уравнений в системе всегда равно числу неизвестных x1, …, xn. Применение явных методов интегрирования требует преобразования системы (1) к нормальному виду, который записывается следующим образом: Переход от системы (1) к (2) предполагает значительное преобразование первоначальной системы с изменением количества уравнений и неизвестных величин. Избежать этого можно, применяя формулу дифференцирования назад (BDF — backward differentiation formula), которая позволяет получить решение непосредственно системы уравнений (1). BDF порядка k аппроксимирует значение x'n+1 — производной от x(t) по времени в момент времени t = tn+1, используя значения xn+1 = x(tn+1) и k предыдущих значений x: xn, xn-1, …, xn-k+1. Для принятых выше обозначений BDF имеет вид: При неравномерном шаге интегрирования коэффициенты BDF должны вычисляться для каждого нового момента времени, формулы расчета коэффициентов приведены в [1] и [2]. При постоянном шаге интегрирования коэффициенты BDF представляют собой константы и не зависят ни от времени, ни от шага интегрирования, их значения можно найти в [3]. При k = 1 коэффициенты BDF равны: α0 = -1 и α1 = 1, формула при этом имеет вид Применение BDF при анализе электрических цепейПерепишем выражение (3), выделив явно слагаемое с j = 0, 1. Индуктивность:
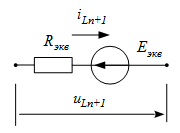
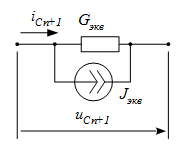
Введя следующие обозначения Для определения Eэкв необходимо знать k предыдущих значений тока iL. 2. Емкость: Аналогично применим BDF для уравнения связи между током и напряжением емкости Соответственно дискретная резистивная схема замещения емкости имеет вид Для определения Jэкв необходимо знать k предыдущих значений тока uC. 3. Взаимная индуктивность: Для элементов со взаимной индуктивностью с согласованным включением Последние два уравнения представляют закон Ома, в которых слагаемые Учитывая, что для напряжений вышеприведенной схемы можно записать
Таким образом применение на каждом шаге интегрирования дискретных резистивных схем замещения реактивных элементов сводит расчет переходного процесса к последовательным расчетам резистивных цепей постоянного тока. Появляющиеся в этих схемах замещения источники ЭДС и токов зависят от предыдущих состояний элементов, которые должны быть известны на глубину равную порядку k применяемой BDF. Поэтому в начале расчета, когда известны только начальные условия для токов в индуктивностях и напряжений на емкостях, возможно применение BDF только порядка k=1, а затем, запоминая необходимое количество состояний элементов, можно последовательно наращивать порядок BDF. Применение порядка k > 6 приводит к неустойчивости метода. Литература 1.↑ Чуа Л.О., Лин Пен-Мин. Машинный анализ электронных схем: Алгоритмы и вычислительные методы. — М.: Энергия, 1980 2.↑ Влах И., Сингхал К. Машинные методы анализа и проектирования электронных схем. — М.: Радио и связь, 1988. 3.↑ Нерретер В. Расчет электрических цепей на персональной ЭВМ. — М.: Энергоатомиздат, 1991. | |
| Просмотров: 353 | | |
| Всего комментариев: 0 | |
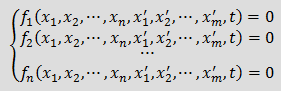 , (1)
, (1)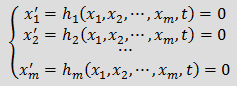 (2)
(2)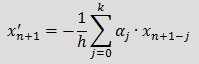 , (3)
, (3)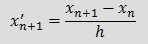 ,
,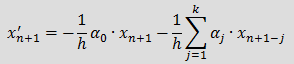
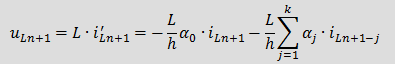 .
.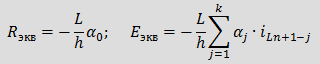 ,
,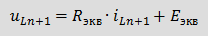 ,
,
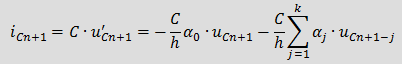 ,
,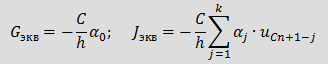 ,
,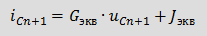 .
.
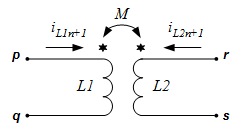
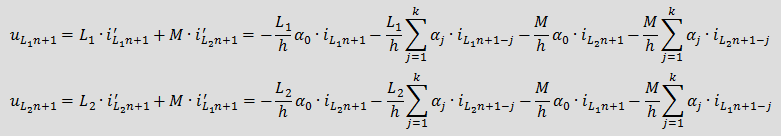 ,
,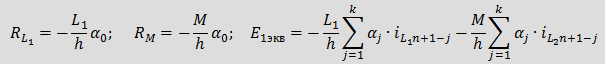
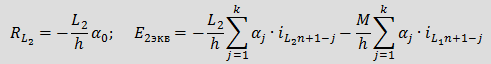 ,
,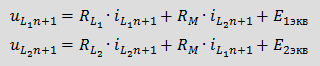 .
.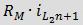 и
и 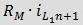 представляют собой управляемые током источники ЭДС.
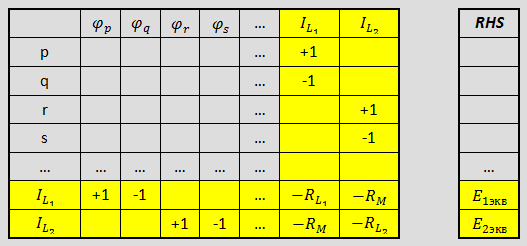
представляют собой управляемые током источники ЭДС.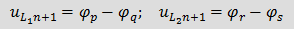 , то в матрице коэффициентов
, то в матрице коэффициентов