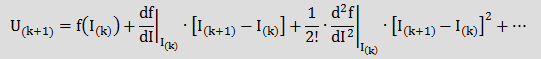В программе LazDiscret2 реализован анализ нелинейных цепей постоянного тока на основе метода Ньютона–Рафсона. Применение этого метода позволяет перейти к линеаризованным уравнениям на каждом шаге итеративного процесса приближения к искомому решению [1].
Покажем этот принцип на примере нелинейного сопротивления, то есть нелинейный резистивный элемент, имеющий однозначную характеристику U=f(I). Так как напряжение на этом элементе зависит только от протекающего по нему тока, то напряжение на k+1 шаге итерации может быть записано [2]: 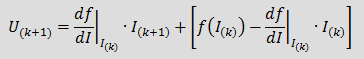 (note1), (note1),
где I(k) и U(k) — ток и напряжение элемента на к–том шаге итерации.
Обозначив 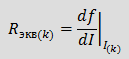 и и 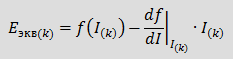 , приходим к выражению закона Ома , приходим к выражению закона Ома
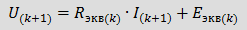 , которому соответствует резистивная эквивалентная схема , которому соответствует резистивная эквивалентная схема
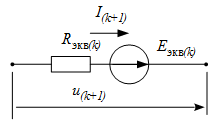
Данная схема является дискретной схемой замещения, так как ее параметры Rэкв(k) и Eэкв(k) корректны только для одного шага итерации.
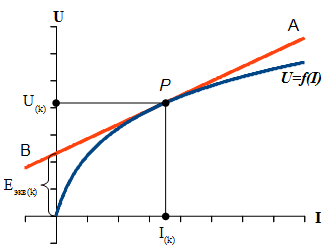
Геометрическая интерпретация получения резистивной эквивалентной схемы приведена на следующем рисунке, на котором показано:
- • U=f(I) — кривая характеристики элемента;
- • P — рабочая точка на к–том шаге итерации;
- • AB — касательная к кривой характеристики, проведенная через точку P.
Касательная AB представляет собой вольт–амперную характеристику линейной цепи, которой может быть заменен нелинейный элемент при изменениях тока вблизи рабочей точки P. С одной стороны тангенс угла наклона ВАХ линейной цепи пропорционален сопротивлению этой цепи, с другой — тангенс угла наклона касательной к кривой графика функции пропорционален производной этой функции, откуда вытекает выражение для Rэкв(k). Выражение для легко Eэкв(k) получается, исходя из геометрических соотношений, которые видны на рисунке.
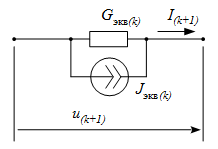
Для нелинейной проводимости, имеющей однозначную характеристику I=f(U), дискретная резистивная эквивалентная схема имеет следующий вид:
Параметры элементов Gэкв(k) и Jэкв(k) этой схемы могут быть найдены по следующим выражениям: 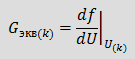 и и 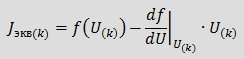 . .
При определении параметров эквивалентных схем необходимо вычисление значения производной функции характеристики нелинейного элемента в текущей рабочей точке. Если характеристика задана в виде таблицы, то встает задача аппроксимации этой характеристики какой-либо функцией, имеющей непрерывную первую производную. В программе LazDiscret2 применяется аппроксимация таблично–заданных характеристик кубическим сплайном [3], в этом случае условие непрерывности первой производной выполняется автоматически.
Предположим, что аппроксимация таблично–заданной нелинейной характеристики выполняется объектом spline. Для этого объект имеет метод:
spline.approximate( const px, py: TOpenFloatArray),
где px, py — массивы аргумента и значений для точек характеристики.
Интерполяция значений характеристики и ее первой производной выполняется методом–функцией этого объекта:
spline.interpolate(ax: TFloat; out dsp: TFloat): TFloat;,
которая возвращает в качестве результата значение характеристики при значении аргумента ax, а также значение первой производной в этой точке в параметре–переменной dsp.
Алгоритм расчета нелинейной цепи постоянного тока при использовании дискретных резистивных моделей упрощенно выглядит следующим образом:
//отметка о необходимости установки начального значения
modeSet += initValue;
iterCount := 0; //счетчик итераций
repeat
//формирование матриц ММУП
matrixSetup;
//расчет уравнений ММУП
matrixSolve;
//напряжений и токов элементов
compute;
//проверка сходимости
if convergence_check then break;
iterCount += 1;
modeSet -= initValue;
until iterCount < DCIterLimit;
if iterCount >= DCIterLimit then error; //превышение макс. числа итераций
Соответствующие процедуры для модели нелинейного сопротивления имеют следующий вид:
matrixSetup
if initValue in modeSet then
//установка начального значения в качестве текущего
inew := initialValue;
//интерполяция
ubk := spline.interpolate(inew, reqk);
//расчет эквивалентной ЭДС
eeqk := ubk - reqk * inew;
//формирование матриц ММУП
ymat[pnode, eqnN] := 1.0; ymat[nnode, eqnN] := -1.0;
ymat[eqnN, pnode] := 1.0; ymat[eqnN, nnode] := -1.0;
ymat[eqnN, eqnN] := -reqk;
rhs[eqnN] := eeqk;
compute
unew := rhs[pnode] - rhs[nnode]; //расчет напряжения на ветви
iold := inew; //сохранение предыдущего тока
inew := rhs[eqnN]; //определение нового тока
convergence_check: boolean
tol := relTol * (max(abs(iold), abs(inew))) + absTol;
result := abs(inew - iold) < tol;
Для модели нелинейной проводимости, соответственно
matrixSetup
if initValue in modeSet then
//установка начального значения в качестве текущего
unew := initialValue;
ibk := spline.interpolate(unew, geqk);
if initValue in modeSet then
inew := ibk;
//расчет эквивалентного истоника тока
jeqk := ibk - geqk * ubk;
//формирование матриц ММУП
ymat[pnode, pnode] := geqk; ymat[pnode, nnode] := -geqk;
ymat[nnode, pnode] := -geqk; ymat[nnode, nnode] := geqk;
rhs[pnode] := -jeqk;
rhs[pnode] := jeqk;
compute
unew := rhs[pnode] - rhs[nnode]; //расчет напряжения на ветви
iold := inew; //сохранение предыдущего тока
inew := geqk * unew + jeqk; //определение нового тока
Процедура проверки сходимости полностью совпадает аналогичной процедурой для модели нелинейного сопротивления.
| (note1) |
Приведенное выражение представляет собой первые два члена ряда Тейлора для f(I) относительно точки I(k): 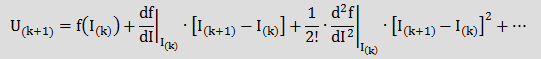 |
Назад
Литература:
1.↑ Чуа Л.О., Лин Пен-Мин. Машинный анализ электронных схем: Алгоритмы и вычислительные методы. — М.: Энергия, 1980.
2.↑ L. W. Nagel. SPICE2: A computer program to simulate semiconductor circuits. Univ. of California, Berkley, ERL Memo ERL M520(May), 1975.
3.↑ Нерретер В. Расчет электрических цепей на персональной ЭВМ. — М.: Энергоатомиздат, 1991.
| 
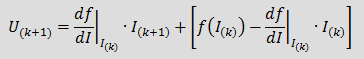
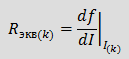 и
и 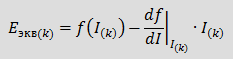 , приходим к выражению закона Ома
, приходим к выражению закона Ома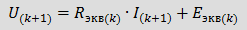 , которому соответствует резистивная эквивалентная схема
, которому соответствует резистивная эквивалентная схема
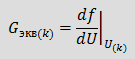 и
и 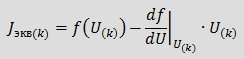 .
.